90 Degree Counterclockwise Rotation Formula

The costless online calculator will rotate the given point around some other given bespeak (counterclockwise or clockwise), with steps shown. We can find the rotation of the points in degrees or in radian, there tin can exist clockwise and the anticlockwise rotation in X-Y aeroplane.

The rotations calculator uses the transformed point rotation formula and the Rotation matrix method to detect new rotation coordinates.

Let'southward endeavor to understand what is the concept of rotation and how it transforms the coordinates of a rotating object.

What is Meant past Rotation?

Rotation is a movement effectually an axis and by rotation geometry nosotros define that:

"Rotation is a move of an object around the eye of an axis."

In real life we can understand the rotational movement by studying the move of the Earth. We know the Earth rotates around its axis in existent life. When an object rotates effectually its axis at that place are four types of transformation happen:

These transformations are:

Rotational
Reflection
Translation
Resizing

Here we are studying the rotational transformation of an object when it rotates around the stock-still centrality.

Rotation Formula:

The Rotation fo rmula can exist used to c alculate the coordinates of the Cartesian coordinates or in the x-y-plane. We can rotate the angle (θ) past rotating a point around the x-centrality. Nosotros tin motion the object in the clockwise and in the anticlockwise directions.

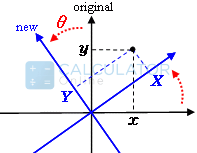
Rotational Vector
The unproblematic formula for the "X" and the "Y" coordinate is equally follows:

For the x-centrality graph rotation, we have the formula:

X=xcos(θ)+ysin(θ)

For the Y-axis graph rotation, and transformed co-ordinate:

Y=−xsin(θ)+ycos(θ)

Where

"X" is new "Ten" coordinate:

"Y" is new "Y" coordinate:

"θ" is new "θ" angle of rotation:

Clockwise and AntiClockwise Rotation Rules:

We need to understand that the rotation tin can be done in both Clockwise and AntiClockwise directions. Y'all can find both the Clockwise and AntiClockwise directions of rotation by the rotation calculator. The most common rotations are normally ninety°, 180° and 270°. The clockwise rotation usually is indicated past the negative sign on magnitude. So the cooperative anticlockwise implies positive sign magnitude.In that location are specific clockwise and the anticlockwise rotation rules and we can effigy out the coordinate airplane by the following tabular array:

Type of Rotation	A point on the Image	A bespeak on the Image after Rotation
Rotation of 90° (Clockwise)	(x, y)	(y, -x)
Rotation of 90° (Counter Clockwise)	(x, y)	(-y, x)
Rotation of 180° (Both Clockwise and Counterclockwise)	(10, y)	(-x, -y)
Rotation of 270° (Clockwise)	(ten, y)	(-y, x)
Rotation of 270° (Counter Clockwise)	(10, y)	(y, -10)

Rotational Matrix:

A rotational matrix is a transformed matrix we get in the Euclidean space(based on dimension and coordinates). In an X-Y plane, the matrix can rotate in a matrix "R" rotate in the anticlockwise direction and make an bending "θ". The matrix "R" can be represented equally follows:

$$ \begin{array}{50}R=\begin{bmatrix} cos\ \theta & -sin\ \theta\\ sin\ \theta & cos\ \theta \end{bmatrix}\end{array} $$

We can perform all the rational matrix operations by the aid of the rotation calculator.

Rotational Symmetry:

In the rotations geometry, every shape has a specific rotational symmetry. These shapes tin can exist Foursquare, Circle, or Rectangle etc. We need to understand every geometric shape or polygon has rotational symmetry. The polygon rotates precisely around its center of gravity and then appears precisely before the rotation.

Nosotros are presenting the society of symmetry of Geometric rectangular shape and how it rotates effectually a point centre of gravity or the rotational axis:

Rotational Example:

We are presenting the real life example of the rotation around the centrality of the rotation.
Rotational Example

The ceiling fans rotate around an axis of rotation and we accept represented it.
The door rotates around the axis of symmetry.

Working of the Rotation Calculator:

The point rotation calculator executes the original points and transforms them into the new Rotionation axis.

Input:

Enter the point of rotation
Select the angle and desired unit
Choose the direction of the rotation
Hit the calculate button

Output:

The rotation calculator swiftly finds the rational points by the rotational formula and by the matrix rotational method:

The transformed points are displayed
The Matrix rational effect is likewise shown

FAQs :

Is rotation in the transformation process?

Rotational coordinates are actually the transformed points and the new position of the object is predicted past the point rotation calculator.

What is rotation in Mathematics?

The rotations are transformations in mathematics , and the rotation of an object is found by the rotational centrality effectually a stock-still or a given signal.

Are the Rotations ane dimensional or non?

The rotations are non one dimensional, it can be clockwise and anti-clockwise. We tin can find the clockwise and anticlockwise rotational points past the rotation calculator counterclockwise.

Are the rotations and revolutions the same?

Yes, both terms are the aforementioned and synonymous. Information technology should be articulate to us that one revolution is equal to 360 degrees. The rotations around any given degree can exist plant by the rotate points calculator.

What is the difference between the point of rotation and angle of rotation?

The points of rotation are the derived or the transformed points calculated by the rotation calculator. The angle of the rotation is the angle around which the object rotates. Information technology tin be measured in degrees or radians.

Conclusion:

The transformed points of the rotation actually predict the expected rotational path of an object accurately. This calculation is essential to notice the path of a rotated object, we practise utilise the axis of symmetry of various geometric shapes.Different shapes have diverse axes of rotation and we find the points of rotation according to their axis of symmetry. The rotation geometry is applied on various geometrical shapes.

References:

From the source of the Wikipedia: Rotation,Mathematics

From the source of the Mathsisfun: Rotation ,Try it Yourself